最終更新 2008.12.9
現在判明している誤りは以下の通りです。
以下の誤りは POD (Print on Demand) 版においては修正されています。
◆ p.30 2.1節 上から3行目
誤 : (Hy, Ex, Ey のみを含む)
正 : (Hy, Ex, Ez のみを含む)
◆ p.65 式(3.2) の手前の式
誤 : 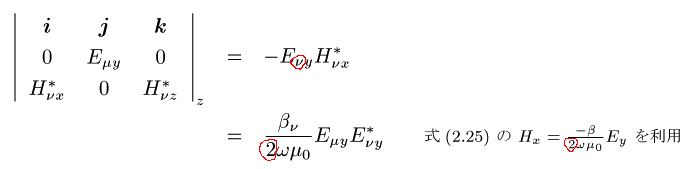
正 : 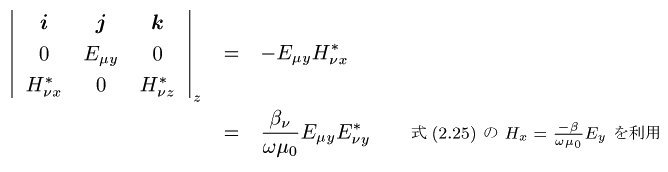
◆ p.67 式(3.14) と (3.15) の間の式
誤 : 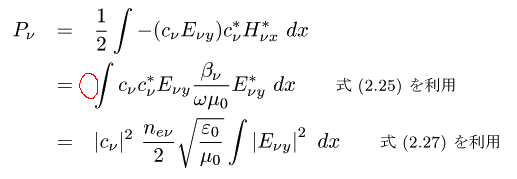
正 : 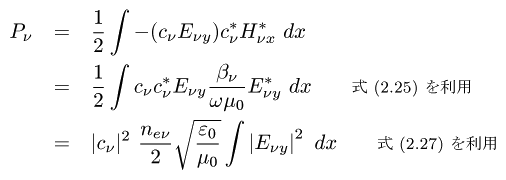
◆ p.77 上から2行目
誤 : 本章における全ての説明は
正 : 本章におけるほとんどの説明は(4.4 節を除く)
◆ p.122 式(5.36)
誤 : 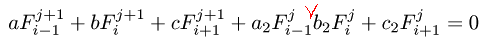
正 : 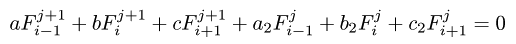
◆ p.123 表 5.1 中の Pade(2,2) 式の定式化
誤 : 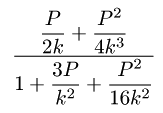
正 : 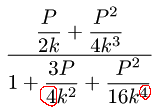
◆ p.145 上から 6 〜 7 行目
誤 : 図6.1(b) のように光の波長のオーダーの周期で屈折率が周期的に変化する構造をグレーティングという。
正 : 図6.1(b) のように屈折率が周期的に変化する構造をグレーティングという。
< 解説 >
グレーティングにおける 2 つのモードの結合条件は p.155 (6.35a) のように
なります。以下に示します。
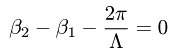
β1 と β2 は 2 つのモードの伝搬定数、Λ はグレーティングの周期です。 これを、
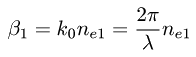
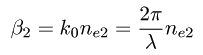
を利用して置換します。ここで、λ は真空中の波長、 ne1 と ne2 は結合する 2 つのモードの等価屈折率です。その結果、
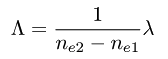
が得られます。
z の正方向へ進むモードと z の負方向へ進むモードが結合するとき、ne1 と ne2 の 符号は逆になり、ne1 と ne2 の値はどちらも 1.5 程度 (シリカガラスの屈折率) ですから、 グレーティングの周期は λ/3 程度の値 ( = 導波路中の波長の 1/2 程度) になります。 これを短周期グレーティングと呼びます。
z の正方向へ進む 2 つのモードが結合するとき (例えば 0 次モードと 1 次モードが結合する、 あるいはファイバにおいてコアモードとクラッドモードが結合する)、 等価屈折率の差は 0.001 〜 0.01 程度 のオーダーの数値になります。このとき、グレーティングの周期は 100λ 〜 1000λ のオーダーに なります。これを長周期グレーティングと呼びます。
このように、グレーティングの周期は、逆方向に進むモード同士が結合するときは、 導波路中の波長の 1/2 程度のオーダーになり、同方向に進むモード同士が結合するときは、 波長の 100〜1000 倍のオーダーになります。
◆ p.149 式(6.19)
誤 : 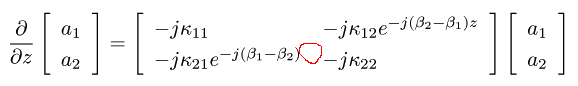
正 : 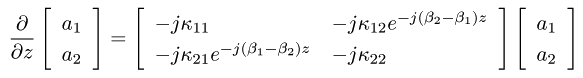
◆ p.232 式(6) の手前の行中の式 (ベクトルであるべき A がスカラになっている)
誤 : 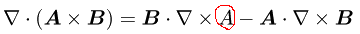
正 : 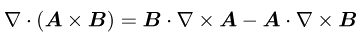
◆ p.233 真中の上の方の文章
誤 : ここで ^ は x, y のだけの関数
正 : ここで ^ は x, y だけの関数